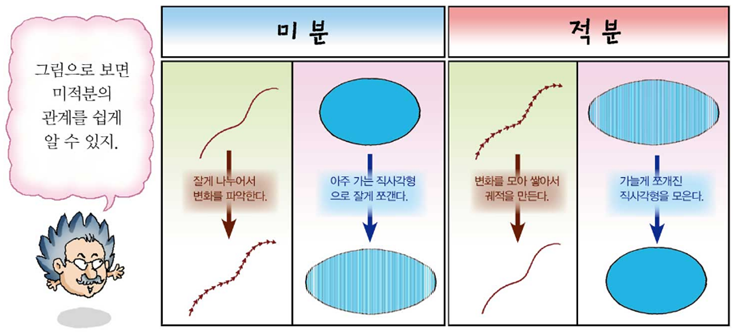
적분[적분]은 뜻대로 나누어진 것을 쌓는다는 뜻입니다.미분이 잘게 쪼개서 변화를 알아보는 것이었다면 면적분은 그렇게 잘게 쪼개진 것을 쌓는다는 뜻입니다.따라서 미분과 적분은 항상 같이 다니면서 미적분이라고 부르게 되었습니다.

미분은 17세기 영국의 뉴턴과 독일의 라이프니츠가 발명한 것입니다. 하지만 항상 함께 다니는 역연산 관계의 적분은 이보다 훨씬 앞선 지금으로부터 약 2천 년 전에 만들어진 개념입니다.
고대 이집트에서는 세금을 부과하여 도시를 건설하기 위한 측량술이 발달하였는데, 이를 고대 그리스로부터 받아들여 기하학을 발전시켰습니다.기원전 4세기경 고대 그리스 수학자 에우독소스는 곡선도형의 넓이를 내접하는 작은 직사각형을 이용하여 넓이를 구했는데, 이것이 적분의 개념과 유사한 것이었습니다.

그리고 기원전 3세기경 유명한 아르키메데스는 더 적분 개념에 가까운 방식으로 곡선 도형의 넓이를 구했지만 무한 개념을 인정하지 않은 그리스 수학자들과 마찬가지로 완전한 적분 개념인 ‘극한’을 이끌어내지 못했습니다.

극한 개념을 처음 적용한 사람은 17세기 수학자이자 천문학자인 케플러입니다.케플러는 원의 넓이를 구하기 위해 원의 중심을 삼각형의 정점으로 하는 무수한 삼각형의 합으로 여겼습니다.

그리고 삼각형 바닥의 길이가 작게 자를수록 삼각형 넓이의 합이 원의 넓이에 가까워지는 것을 알 수 있었습니다.
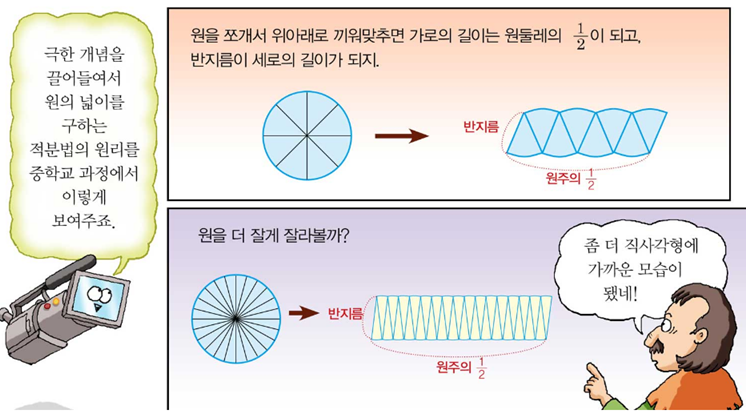
이러한 케플러 방식은 중학교 수학에서도 나오는데, 그것이 바로 원의 넓이를 구하는 방식을 적분의 개념으로 설명하는 것입니다.

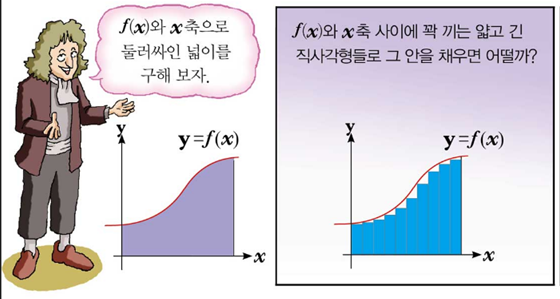
그럼 현대의 적분 개념에 대해 살펴보겠습니다.y=f(x)라는 함수와 x축으로 둘러싸인 도형의 넓이를 구하기 위해 그 안을 얇고 긴 직사각형으로 메워서 면적을 구하는 방식을 ‘구분구적법’이라고 합니다.
이때 막대의 높이는 y값 즉 f(x)가 되고, 막대의 밑변 길이를 0에 근접하도록 극한까지 보냈을 때를 dx라고 한다면 작게 자른 직사각형의 넓이는 f(x)xdx가 됩니다.그리고 그런 작은 직사각형의 넓이를 늘린다는 뜻의 기호 ‘인테그럴’을 사용해서 적분을 표시합니다.

이것을 ‘부정적분’이라고 하고, ‘부정적분’과 달리 일정 구간의 넓이를 구하는 것을 ‘정적분’이라고 합니다.
적분의 개념은 간단했지만 실제로 이를 계산하기에는 매우 복잡하고 어렵습니다.이런 고민을 한꺼번에 해결해 준 것이 뉴턴입니다. 뉴턴은 미분과 적분이 역연산 관계에 있음을 간파하고 계산하기 쉬운 미분을 하여 역산을 하여 적분값을 구하는 방법을 알아냈습니다.

수학 발전의 획기적인 발판이 된 미적분 발명은 보통 뉴턴으로 알고 있는데, 10년 정도 늦게 라이프니츠 또 독자적으로 발명했습니다.이런 이유로 영국 수학계와 독일을 중심으로 한 유럽 수학계는 미적분 발명의 우선권이 누구에게 있는지를 놓고 100년간 논쟁이 벌어졌습니다.

이 기간 영국 수학계는 유럽 수학계와 교류가 단절돼 미적분 발전이 잘 이뤄지지 않았지만 유럽 수학계는 라이프니츠가 만든 미적분 기호 덕분에 미적분이 크게 발전할 수 있었고 현재 사용하고 있는 미적분 기호는 라이프니츠가 만들어낸 것입니다.

마지막으로! 다른 수학 개념과 달리 미적분을 ‘발견’이 아닌 ‘발명’이라는 이유는 일반적인 수학 개념의 발견은 자연 현상을 숫자와 기호로 바꾸어 표현하는 방법을 알아냈다는 의미로 ‘발견’이라는 단어를 사용합니다. 그러나 미적분은 자연과 사회의 변화를 관찰하고 예측하는 도구로 사용될 수 있기 때문에 ‘발명’이라는 용어를 사용하고 있습니다.

출처 : http://www.ebsmath.co.kr/url/go/23500 우리가 지금 공부하고 있는 수학은 과연 언제부터 있었을까요? 갑자기 어느 날 갑자기 생겨났을까요? 역사적 상황과 배경에 따라 수학이 어떻게 탄생하고 발전해 왔는지를 밝혀봅시다. 그러면 수학이 동떨어진 학문이 아니라 문명을 발전시켜 나가는 데 단단한 발판이었음을 깨닫게 될 것입니다! www.ebsmath.co.kr